应用密码学

摘要：通过本学期的《应用密码技术》课程，我系统地学习了密码学的相关知识，对信息加密技术有了一个新的认识，本文对本学期我所做的密码技术笔记做一个整合

绪论

密码学的基本概念

密码学(Cryptology)：

研究信息系统安全保密的科学。

密码编码学(Cryptography)：

研究对信息进行编码,实现对信息的隐蔽。

密码分析学(Cryptanalytics) ：

研究加密消息的破译或消息的伪造。

消息被称为明文(Plaintext)。

用某种方法伪装消息以隐藏它的内容的过程称为加密(Encrtption)，被加密的消息称为密文(Ciphertext)，而把密文转变为明文的过程称为解密(Decryption)。

密码算法：

用于加密和解密的数学函数。 密码员对明文进行加密操作时所采用的一组规则称作加密算法(Encryption Algorithm)。\所传送消息的预定对象称为接收者(Receiver)。接收者对密文解密所采用的一组规则称为*解密算法(Decryption Algorithm)。

加密算法基本原理

代替：明文中的元素映射成另一个元素 置换 ：重新排列 要求：不允许信息丢失，即算法可逆

基于密钥的算法，按照密钥的特点分类：

对称密码算法(symmetric cipher)：加密密钥和解密密钥相同，或实质上等同，即从一个易于推出另一个。又称秘密密钥算法或单密钥算法。 非对称密钥算法(asymmetric cipher)：加密密钥和解密密钥不相同，从一个很难推出另一个。又称公开密钥算法(public-key cipher) 。

密码分析破解类型：

1. 唯密文攻击 密码分析者仅知道有限数量用同一个密钥加密的密文
2. 已知明文攻击 密码分析者除了拥有有限数量的密文外，还有数量限定的一些已知“明文—密文”对
3. 选择明文攻击 密码分析者除了拥有有限数量的密文外，还有机会使用注入了未知密钥的加密机，通过自由选择明文来获取所希望的“明文—密文”对。
4. 选择密文攻击 密码分析者除了拥有有限数量的密文外，还有机会使用注入了未知密钥的解密机，通过自由选择密文来获取所希望的“密文—明文”对。
5. 选择文本攻击

古典密码体制

替换密码

单字符单表替换密码

恺撒密码(Caesar Cipher)

已知的最早（也是最简单的方式）的简单替代密码是朱里斯.恺撒所用的密码。恺撒密码是把字母表中的每个字母用该字母后面第3个字母进行代替。例如： 明文：meet me after the toga party 密文：PHHW PH DIWHU WKH WRJD SDUWS 既然字母表是循环的，因此Z后面的字母是A。能够通过列出所以可能性定义如下所示的变换：

移位密码(Shift cipher）

对每个明文字母p，恺撒加密可转化为移位密码，其中加密算法： C = E(p) = (p＋k) mod (26)，其中k在1～25之间取值。 解密算法是：p = D(C) = (C－k) mod (26) 如果已知密文是恺撒密码，则使用强行攻击密码分析容易取得结果 直接对所有25个可能的密钥进行尝试。

仿射密码算法

P = C = Z~26~ K = (a，b) ∈K = Z~26~×Z~26~ 加密 y = e~K~(x) = (ax＋b) mod 26 要求唯一解的充要条件：gcd(a,26)=1 解密 d~K~ (y) = (y – b) / a mod 26 = (y – b) a^-1^ mod 26

程序实现

if ((byte) m.charAt(i) > 96) {
	tmp = (char) (97 + ((m.charAt(i) - 'a') * k1 + k0) % 26);
	} else 
	tmp = (char) (65 + ((m.charAt(i) - 'A') * k1 + k0) % 26);
	n.add(tmp);

单字符多表替换密码

Vigenére密码：

是一种多表移位代替密码 设d为一固定的正整数，d个移位代换π=(π1,π2,…,πd) 由密钥序列K=(k1,k2,…,kd)给定，第i+td个明文字母由密钥ki决定 ek(xi+td) = (xi+td + ki) mod q = y，dk(yi+td) = (xi+td－ki) mod q = x 例子：q=26, x=polyalphabetic cipher, K=RADIO 明文 x= p o lya l phab e t i cc i pher 密钥 k= R ADIO RADIO RADIO RADIO
密文 y= GOOGO CPKTP NTLKQ ZPKMF

程序实现

if (judgeCase(noSpace.get(i)) > 0) {
	cipher.add((char) (judgeCase(noSpace.get(i)) + (this.getIndex(noSpace.get(i)) + keySets.get(i)) % 26));
} else 
cipher.add(noSpace.get(i));

Hill密码：

基于矩阵的线性变换，由数学家Lester Hill于1929年研制 Z26上的线性变换 例：x＝（x1，x2），y＝（y1，y2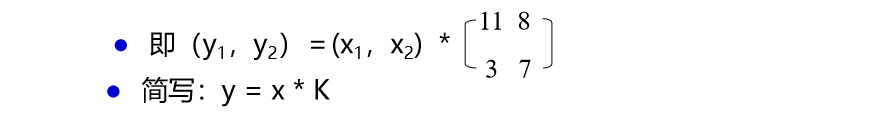） 定义：y~1~＝11x~1~＋3x~2~ mod 26，y~2~＝ 8x~1~＋7x~2~ mod 26

Playfair 密码

Playfair：将明文中的双字母组合作为一个单元对待，并将这些单元转换为密文的双字母组合。 5×5变换矩阵： I与J视为同一字符 加密规则：按成对字母加密 相同对中的字母加分隔符(如x)

程序实现

for (group x : plainGroup) {
	char key_1, key_2;
		if (x.i_row == x.j_row) {
			key_1 = (keyList.get(x.i_row * 5 + (x.i_column + 1) % 5));
			key_2 = (keyList.get(x.j_row * 5 + (x.j_column + 1) % 5));
            } else if (x.i_column == x.j_column) {
			key_1 = (keyList.get((x.i_row + 1) % 5 * 5 + x.i_column));
			key_2 = (keyList.get((x.j_row + 1) % 5 * 5 + x.j_column));
            } else if (x.i_row == x.j_row) {
			key_1 = (keyList.get(((x.i_row + 1) % 5) * 5 + x.i_column));
			key_2 = (keyList.get(((x.j_row + 1) % 5) * 5 + x.j_column));
            } else {
			key_1 = (keyList.get(x.j_column + x.i_row * 5));
			key_2 = (keyList.get(x.j_row * 5 + x.i_column));
            }
  System.out.println(keyList.get(x.i_row * 5 + x.i_column) + " --> " + key_1);
	System.out.println(keyList.get(x.j_row * 5 + x.j_column) + " --> " + key_2);
	cipherList.add(key_1);
	cipherList.add(key_2);}

换位密码

列换位 明文按照密钥个数排列，然后再按照在字母表中的顺序变换列的顺序变换列的顺序，最后按照列的顺序写出密文

周期换位 明文按照密钥个数分组，然后按照密钥在字母表中的顺序变换组内字母的顺序

分组密码体制

分组密码是将明文消息编码表示后的数字(简称明文数字)序列，划分成长度为n的组(可看成长度为n的矢量)，每组分别在密钥的控制下变换成等长的输出数字(简称密文数字)序列。

特点

• 明文被分为固定长度的块，即分组，分组一般为64比特，或者128比特
• 对每个分组用相同的算法和密钥加/解密
• 密文分组和明文分组同样长

Feistel 密码结构

在 Feistel 网络中，加密的各个步骤称为轮 (round). 整个加密过程就是进行若干次轮的循环

上面的两个方框表示 Feistel 网络中一轮的输入(明文)。 输入的数据被等分为左右两半分别 进行处理 。 在图中，左半部分写作 “左侧”， 右半部分写作“右侧” 。

下面的两个方框表示本轮的输出(密文)。 输出的左半部分写作“加密后的左侧”，右半部 分写作“右侧”。

中间的”子密钥’指的是本轮加密所使用的密钥 。 在 Feistel 网络中，匈一轮都需要使用一 个不同的子密钥? 巾千子密钥只在一轮中使用，它只是一个局部密钥 ， 因此称为子密钥 (subkey )。

轮函数 的作用是根据’`右侧”和子密钥生成对“左侧”进行加密的比特序列，它是密码系统的核心 。 将轮函数的输出与“左侧”进行 XOR 运算，其结果就是“加密后的左侧” 。 也就是说，用 XOR 将轮函数的输出与“左侧”进行了合并 。 的”右侧” 。

一轮的具体计算步骤如下 。

1. 将输入的数据等分为左右两部分 。
2. 将输入的右侧直接发送到输出的右侧 。
3. 将输入的右侧发送到轮函数 。
4. 轮函数根据右侧数据和子密钥，计算出 一串看上去是随机 的比特序列 。
5. 将上一步得到的比特序列与左侧数据进行 XOR运算， 并将结果作为加密后的左侧 。

数据加密标准 DES

数据加密标准(Data Encryption Standard，DES)是至 今为止使用最为广泛的加密算法。

加密和解密

DES 是一种将 64 比特的明文加密成 64 比特的密文的对称密码算法，它的密钥长度是 56 比 特 。 尽管从规格上来说， DES 的密钥长度是 64 比特，但由于每隔 7 比特会设置一个用于错误检查的比特，因此实质上其密钥长度是 56 比特 。 DES 是以 64 比特的明文 (比特序列) 为 一个单位来进行加密的，这个 64 比特的单位称为分组 。 一般来说，以分组为单位进行处理的密码算法称为分组密码 (block cipher), DES就是分组密码的一种 。 DES 每次只能加密 64 比特的数据，如果 要加密的明文比较长，就需要对DES加密进行迭 代(反复)，而迭代的具体方式就称为模式 (mode)。

DES的变形

• 二重DES
• 三重DES
  • DES-EEE3
  • DES-EDE3
  • DESEEE2
  • DES-EDE2

程序实现

public char[] encode(char[] plaintextBytes, char[][] subKeys) {
      // 初始置换
      char[] chars = ArrayUtil.disruptArray(plaintextBytes, DESConstants.IP);
      int length = chars.length;
      String binaryArrayStr = String.valueOf(chars);
      char[] left = binaryArrayStr.substring(0, length / 2).toCharArray();
      char[] right = binaryArrayStr.substring(length / 2).toCharArray();
      char[] coreEncrypted, xorResult;
      // 进行16轮加密运算
      for (int i = 0; i < 16; i++) {
         coreEncrypted = coreEncrypt(right, subKeys[i]);
         xorResult = String.valueOf(ArrayUtil.xor(left, coreEncrypted, 48)).substring(16).toCharArray();
         left = right;
         right = xorResult;
      }
      char[] calResult = ArrayUtil.concat(right, left);
      // 进行逆初始置换
      return ArrayUtil.disruptArray(calResult, DESConstants.inverseIP);
   }

高级加密标准 AES

AES (Advanced Encryption Standard) 是取代其前任标准 (DES) 而成为新标准的 一种对称密码算法 。 全世界的企业和密码学家提交了多个对称密码算法作为 AES 的候选，最终在 2000 年从这些候选算法中选出了 一种名为 Rijndael 的对称密码算法，并将其确定为了 AES。

AES算法描述

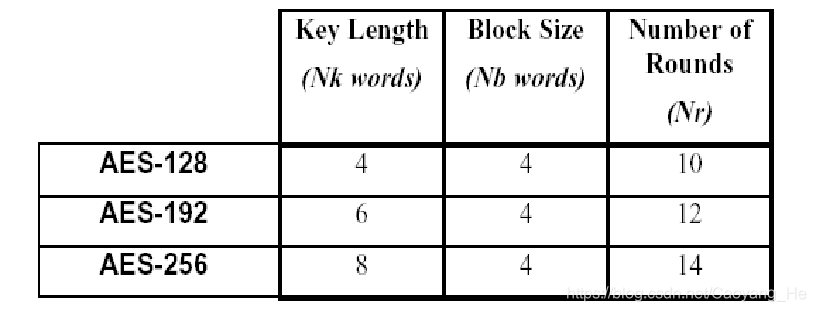
Rijndael算分的明文长度、密钥长度都可以彼此独立的确定为128、192、256bit，因此Rijndael算法可以有9种不同的版本。NIST选中Rijndael算法作为AES算法，限定了明文分组长度为128bit，而密钥长度也可以为128、192、256bit，因而AES有三个版本：AES-128, AES-192, AES-256

AES加密过程

1. 字节代替：使用S盒的字节进行 非线性变换
2. 行移位：根据列数不同每行移动不同的位数
3. 列混合：使用一个固定的矩阵与状态矩阵在有限域$GF(2^8)$上相乘
4. 轮密钥加：将状态矩阵与子密钥矩阵对应位置的字节进行异或操作

SM4 加密算法

继美国将Rijndael算法作为高级加密标准AES、欧洲将Camelia等算法作为NESSIE分组加密标准后，中国国家密码管理局在2006年1月6日发布第7号公告，将我国无线局域网产品的加密算法确定为SM4算法。 该算法明文长度为128bit，密钥长度为128bit。加密算法和解密算法都采用32轮非线性迭代结构。

分组密码工作模式

ECB 模式

CBC模式

CBC工作模式直接使用前一个经过处理后的分组进行异或运算后加密

CFB模式

CFB工作模式 把前一个经过处理的分组经过加密后，再从中取j位，与当前明文分组进行异或运算

OFB模式

OFB工作模式 将前一个分组加密过程中形成的密钥再次加密，然后与明文分组进行异或运 算，并将形成的密钥传到下个分组中

分组填充方式

• Zeros填充：使用数字0填充
• X923填充：最后一个字符记录填充的总字节数
• PKCS7填充：每个填充的字节都记录填充的字节数
• ISO10126填充：随机填充字符，最后一个字节记录填充字节数

非对称密码体制

基本原理

公钥算法基于数学函数而不是基于替换和置换。用户拥有自己的密钥对(K~U~,K~R~)，即（公开密钥，私有密钥） 公钥K~U~公开。

公钥密码学的提出是为了解决两个问题：

• 密钥的分配

• 数字签名

主要特点

• 加密和解密能力分开
• 多个用户加密的消息只能由一个用户解读，（用于公共网络中实现保密通信）
• 只能由一个用户加密消息而使多个用户可以解读（可用于认证系统中对消息进行数字签字）。
• 无需事先分配密钥
• 密钥持有量大大减少
• 提供了对称密码技术无法或很难提供的服务：如与哈希函数联合运用可生成数字签名，可证明的安全伪随机数发生器的构造，零知识证明等

RSA算法

密钥对生成

1. 选择两个大素数p,q, p ≠q （p、q 私有，选定）
2. 计算n=pq(n<2^1024^ ) （n 公开，计算出）
3. 选择整数e，使得gcd(e,Φ(n))=1 （e公开，选定的）
4. 计算d ≡ e^-1^ mod Φ(n) (d保密，计算得出的）
5. 公钥: KU={e,n}, 私钥: KR={d,n}

加密和解密

加密: C = M^e^ mod n (明文M<n) 解密: M = C^d^ mod n

程序实现

// 计算幂的余数
	public static int rsaCore(int a, int b, int c) {
		int r = 1;
		b = b + 1;
		while (b != 1) {
			r = r * a;
			r = r % c;
			b--;
		}
		return r;
	}
	// 互素数判断
	public static boolean func(int x, int y) {
		int t;
		while (y != 0) {
			t = x;
			x = y;
			y = t % y;
		}
		return !(x==1);
	}

DES和RSA性能比较(同等强度)：

数论基础

素数和互素数

称整数p(p>1)是素数，如果p的因子只有±1，±p。 若满足下面2个条件，则称c是两个整数a、b的最大公因子，表示为c=gcd(a, b)。 ① c是a的因子也是b的因子，即c是a、b的公因子。 ② a和b的任一公因子，也是c的因子。 如果gcd(a,b)=1，则称a和b互素。

模运算

设n是一正整数，a是整数，如果用n除a，得商为q，余数为r，用a mod n表示余数r。 如果(a mod n)=(b mod n)，则称两整数a和b模n同余，记为a≡b mod n。 称与a模n同余的数的全体为a的同余类，记为[a]，称a为这个同余类的表示元素。

对比：对称密码体制VS非对称密码体制

对称密码体制的优点

速度快，处理量大，适用于对应用数据的直接加密。 加密密钥长度相对较短,如40比特～256比特。 可构造各种加密体制，如产生伪随机数，HASH函数等。

对称密码体制的缺点

密钥在双方都要一致、保密，传递较难。 大型网络中密钥量大，难以管理，一般需要TTP（KDC）。 密钥需要经常更换 数字签名的问题：传统加密算法无法实现抗抵赖的需求。

非对称密码体制的优点

只有秘密钥保密，公开钥公开。 密钥生命周期相对较长。 许多公钥方案可以产生数字签名机制。 在大型网络上，所需的密钥相对较少。

非对称密码体制的缺点

速度慢，处理量少，适用于密钥交换。 密钥长度相对较长。 安全性没有得到理论证明。

心得体会

在学习密码学之前，我觉得密码学是一个高深的领域，从小在电影中看到的那些密码破译者，都觉得他们很酷。通过本学期《应用密码学》课程，我才真正感受到了密码学的魅力。在透明的网络中，只有将信息安全的加密，才能保证自己的信息不被随意泄漏。密码技术也随着互联网发展而不断进步，在Web3.0时代，使用数字钱包加密成为新的较为可靠的加密方式。

• Previous
  DP动态规划
• Next
  正则表达式